昨天的Physical Review Letters杂志上发表了一篇实验文章《New Determination of the Fine Structure Constant and Test of the Quantum Electrodynamics》,Phys. Rev. Lett. 106, 080801,通过实验测定普朗克常数与 87Rb 原子质量的比值 h/mRb,导出了新的精细结构常数值
α-1=137.035 999 037 (91),
测量的相对不确定度为 6.6×10-10。然后通过量子电动力学理论推导,进而给出了电子磁矩反常因数的值 ae=0.001 159 652 181 13(84),这与之前Gabrielse研究组测定的实验值 ae=0.001 159 652 180 73(28) 相一致。两个值相比较为量子电动力学(QED)理论提供了最严格的检验。同时,高精度的实验也首次证实了μ子和强子对于电子反常磁矩的贡献。
下面我们稍微展开来讨论一下。精细结构常数 α 是物理学中一个重要的无量纲数,是电磁相互作用中电荷之间耦合强度的度量,表征了电磁相互作用的强度,最早是为了解释氢原子光谱结构而引入。精细结构常数将电动力学中的电荷 e、量子力学中的普朗克常数 h、相对论中的光速 c 联系起来,是无法从第一性原理出发导出的无量纲常数,只能通过实验测定。因此,在不同物理领域测定其数值是对理论一致性、自洽性的绝佳检验工具。
此前为止,最精确测量精细结构常数的办法是实验测定电子磁矩的反常因数值 ae,然后再通过复杂的QED理论计算导出 α。哈佛大学的Gabrielse等人最近的实验给出 α 的相对不确定度为3.7×10-10(0.37 ppb),精细结构常数值为
α-1=137.035 999 084 (51),
其中用到的QED计算公式类似下式:
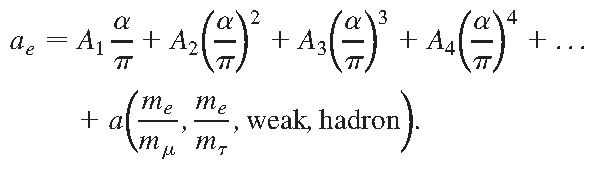
即以 α/π 作冥级数展开,并包含μ子、τ子、弱相互作用以及强子修正项等。具体理论进展可以参考Kinoshita等人的工作Phys. Rev. Lett. 99, 110406 (2007)等等。
而另一种办法,即此文的工作,则是利用如下关系:
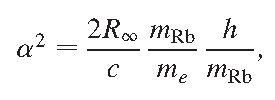
其中 R∞ 是里德伯常数。这样通过测定 h/mRb 即可得出精细结构常数。而此值在实验中可通过测量铷原子吸收一个光子后的反冲速度来确定。具体实验原理可参考此文。
由此,我画一个简单的示意图,大家可以理解其间的关系:
实验测 h/mRb –>> 精细结构常数 α <<– QED理论 –>> 电子磁矩反常因数 ae
我们来看看这两种主要的办法给出的精细结构常数 α 的结果比较,如下图所示
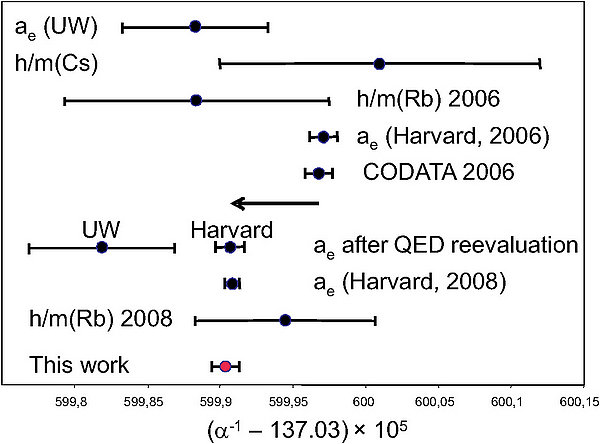
而电子磁矩反常因数 ae 的推导结果以及与以前结果的比较则见下图:
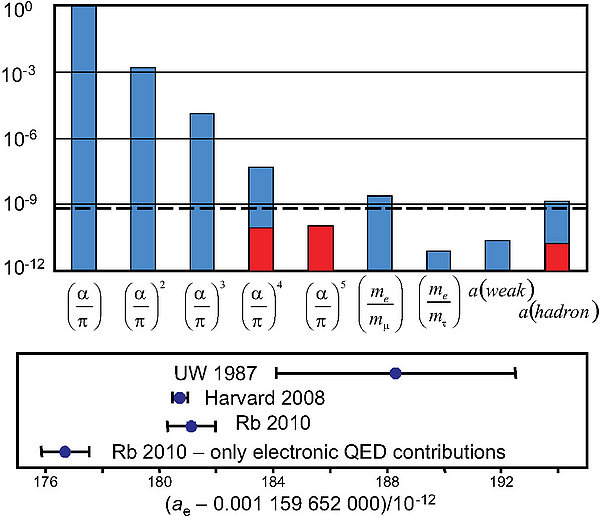
QED公式不同部分的贡献以蓝色柱状图表现,其中红色部分为不确定度。可以看出,如果忽略第一个公式中最后一项μ子、τ子、弱相互作用以及强子修正项的贡献,则当前结果无法与此前得到的结果相一致,由此证实了μ子和强子对于电子反常磁矩具有贡献。
我们知道,电子自旋1/2,由自旋而产生了內禀磁矩,如果假设为点粒子,则其g因子应等于2。而此处反常磁矩的出现,在QED理论计算正确的前提下则意味着电子也可能具有内部结构,或者有可能存在新的暗物质粒子(Phys. Lett. B 661, 287)。这一切,还有待更高精度实验和更准确理论模型计算的验证(因为一个Fortran程序小问题,就导致了很大的误差偏离,可叹啊)。
